Multi-head latent attention

Overview

Multi-head latent attention (MHLA) was developed specifically to tackle the significant memory requirements of the Key Value (KV) Cache during the inference stage of large language models. The KV Cache is crucial because it stores computed keys and values from previous tokens, enabling the model's computation time to grow linearly with the input sequence length, rather than quadratically. However, this cache can consume vast amounts of memory, particularly for large models processing long contexts. For example, a model like DeepSeek R1 or V3 with 128 attention heads and a 100,000 context window could require a KV Cache of 400 GB with the standard Multi-Head Attention (MHA) approach. This high memory usage leads to increased costs and slower inference.

Before MHLA, the main approaches to reduce KV Cache memory were Multi-Query Attention (MQA) and Grouped-Query Attention (GQA).

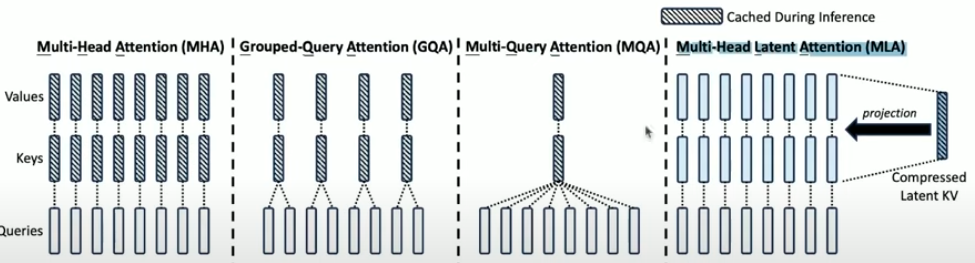
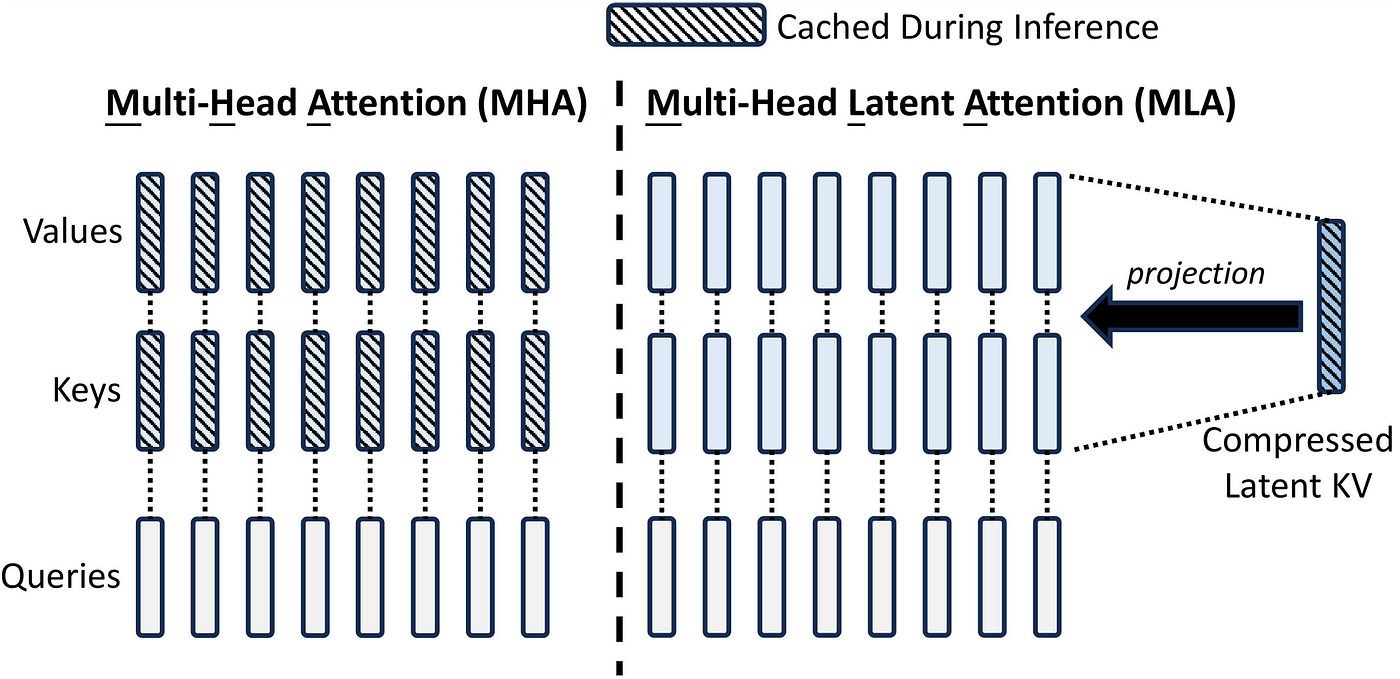
• Multi-Head Attention (MHA): The standard approach. Each attention head has its own distinct weight matrices (WK, WV) and thus produces unique key and value matrices. This requires caching the keys and values for every head, making the KV Cache size directly proportional to the number of attention heads. MHA generally offers the best performance as it allows each head to capture different relationships, but has the largest KV Cache.

• Multi-Query Attention (MQA): All attention heads share the same key and value matrices by using a single set of WK and WV weights for all heads. This drastically reduces the KV Cache size, as you only need to cache the keys and values for effectively one head. MQA offers the smallest KV Cache but suffers from significant performance degradation and reduced context understanding because sharing keys and values limits the diversity across heads.

• Grouped-Query Attention (GQA): A compromise where attention heads are divided into groups, and heads within a group share the same key and value matrices, but heads in different groups use different ones. GQA reduces KV Cache size compared to MHA (by a factor of N/G, where N is heads and G is groups) and improves performance compared to MQA, but its cache size and performance are generally medium, lying between MHA and MQA.

The Goal of Multi-Head Latent Attention

MHLA aims to achieve the "best of both worlds": a low KV Cache size (ideally close to MQA's) and good language model performance (closer to MHA's). To reduce the KV Cache size, the dependency on the number of attention heads (N) and the head dimension (H) in the cache size formula (L*B*N*H*S*2*2) needs to be significantly reduced or eliminated, ideally by reducing the NxH factor. To maintain good performance, the keys and values used by different attention heads need to be distinct, not shared like in MQA or GQA.

The Core Mechanism: Projecting to a Latent Space

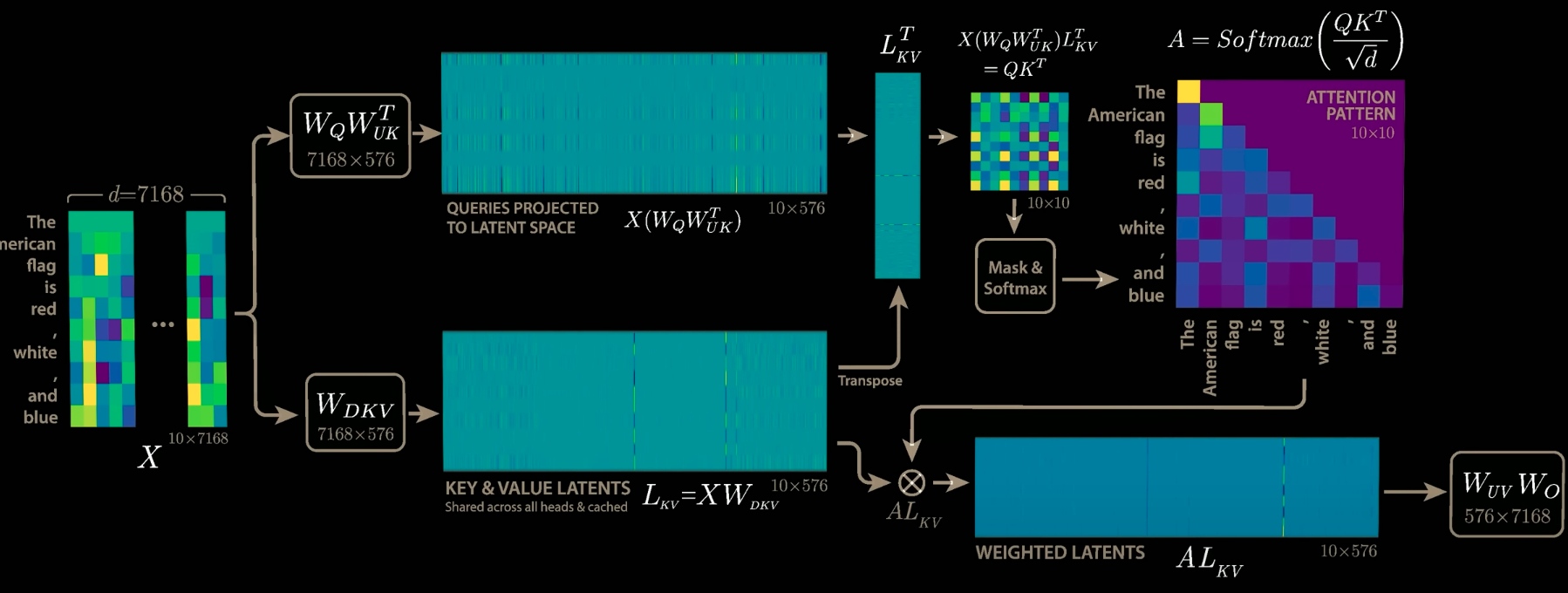
MHLA achieves this balance by introducing a latent space projection. Instead of computing and caching separate keys and values for each head (or group), MHLA computes and caches only one single matrix, which is a projection of the input embeddings into a lower-dimensional latent space. And this single matrix would not have the original dimensions of N*H but rather Ne.

Here's the detailed workflow in MHLA, especially when processing a new token during inference:

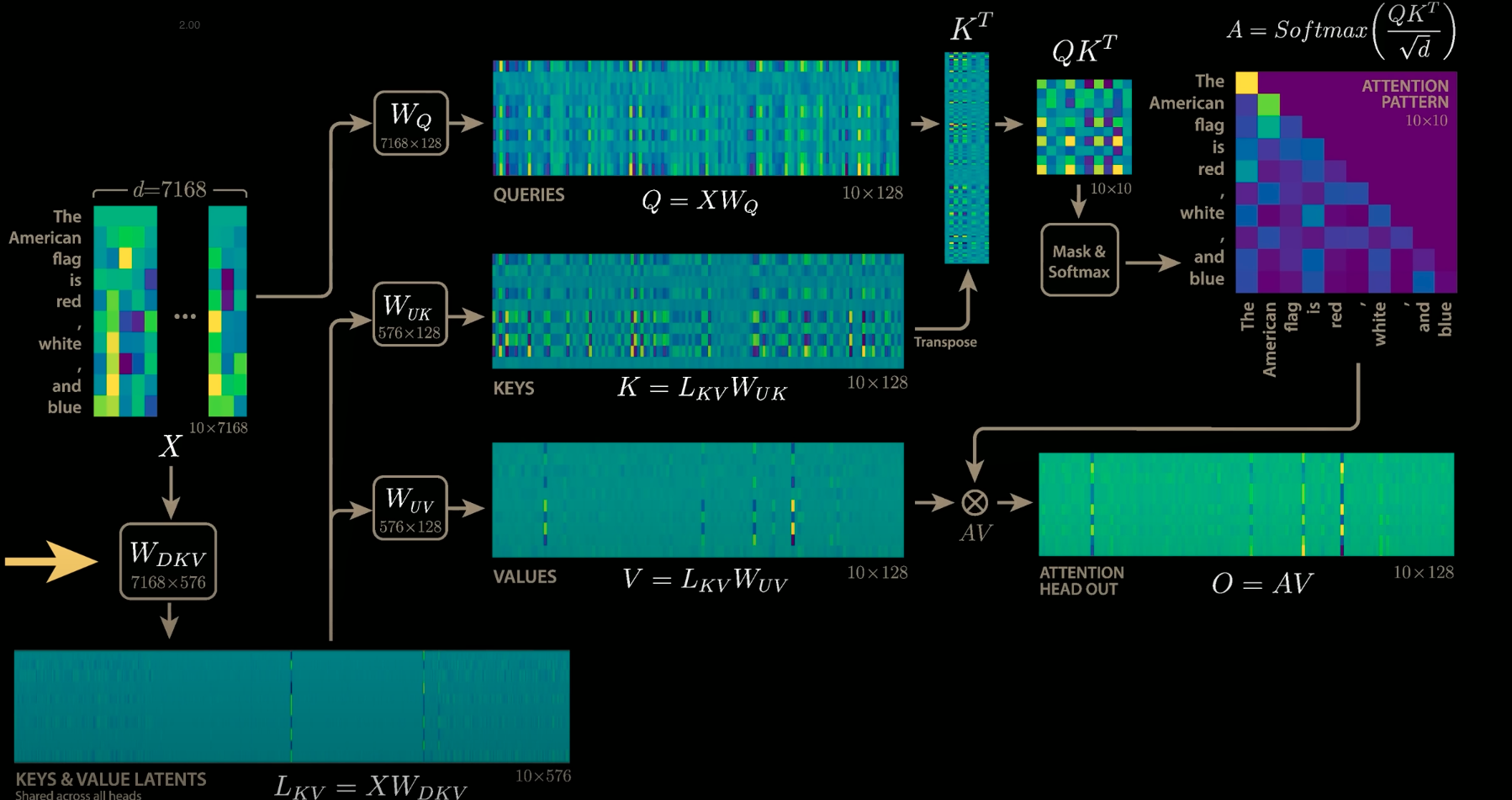
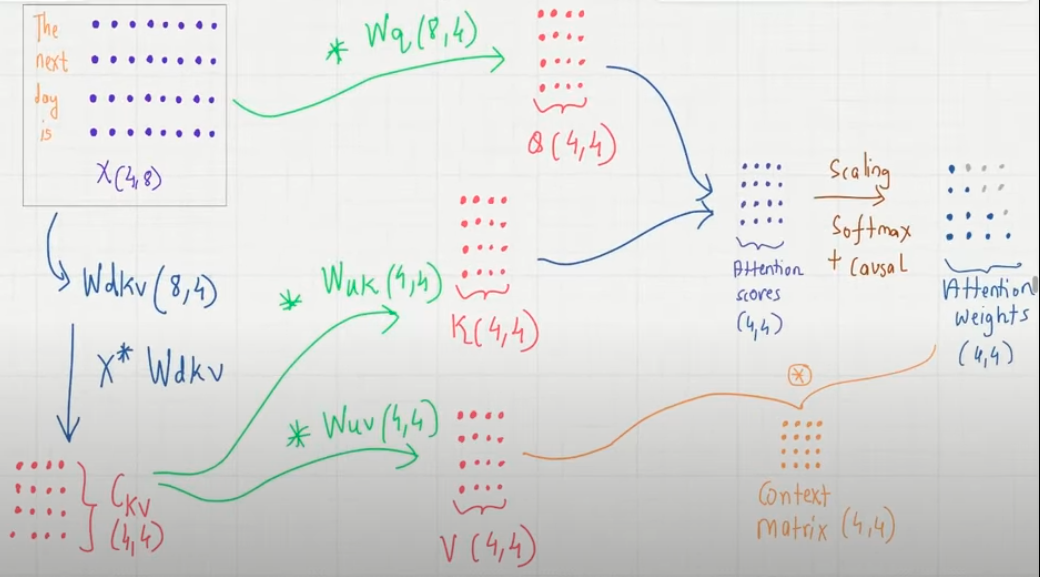
Wk becomes Wuk. (i)

Wv becomes Wuv (ii)

Input X becomes latent matrix Ckv (X * Wdkv) (iii) - This is only the cached part

Q = X * Wq

K = Ckv * Wuk

V = Ckv * Wuv (iv)

1. Input Embedding: The new input token gets its input embedding vector.

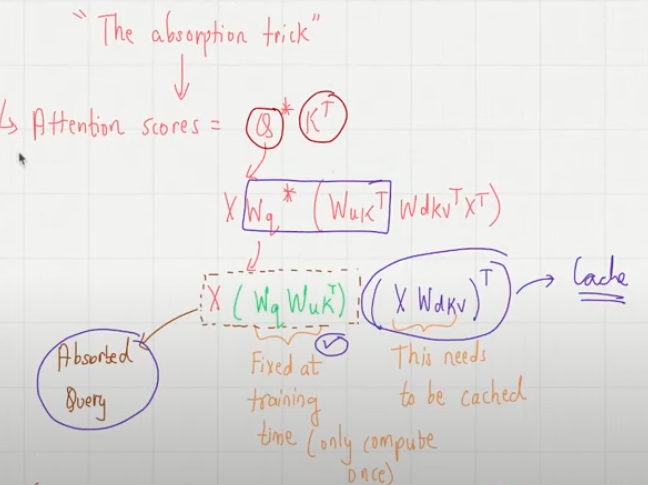
2. Compute Absorbed Query: The input embedding for the new token is multiplied by a pre-computed, fixed matrix which is the result of WQ multiplied by WUK^T. This matrix WQ * WUK^T) is calculated once during pre-training and is not cached. The result is the "absorbed query vector" for the new token.

3. Compute New Latent KV Vector: The input embedding for the new token is multiplied by the WDKV matrix (Weight for Down-projection of KV) as shown in (iii). This WDKV matrix projects the input embedding into the lower-dimensional latent space. The result is the "latent embedding" or "new KV vector" for the new token and is denoted as Ckv - cached KV.

4. Update Latent KV Cache: This new latent KV vector is appended to the existing single cached matrix (CKV), which stores the latent projections for all previous tokens. This updated CKV is the model's KV cache.

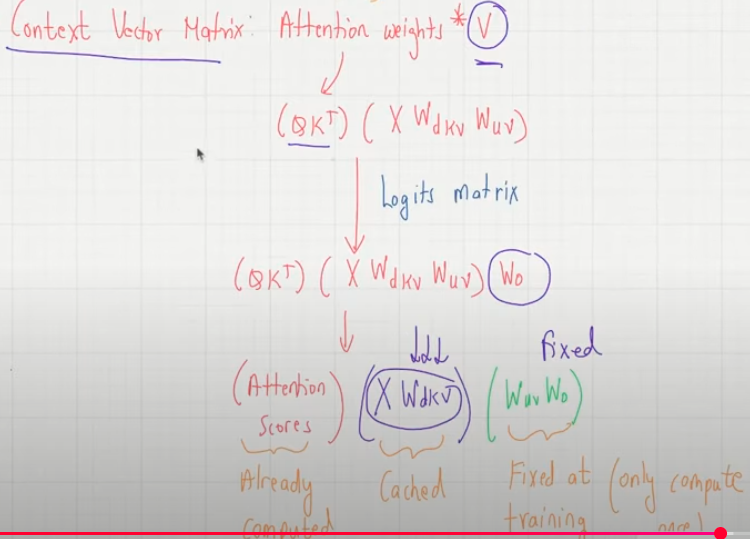
5. Compute Attention Scores: The newly computed absorbed query vector is multiplied by the entire updated latent KV cache (CKV). This calculation directly yields the attention scores for the new token against all previous tokens. This is where the "absorption trick" is realised: by pre-multiplying WQ and WUK^T, the need for the explicit Keys matrix (K) in the attention score calculation (Q * K^T) is hidden; the necessary information is now implicitly used via the absorbed query and the latent cache.

6. Compute Attention Weights: The attention scores are scaled and passed through a softmax function to get the attention weights.

7. Compute Values Matrix: The same updated latent KV cache (CKV) is multiplied by the WUV matrix (Weight for Up-projection of Values) as in (iv). This WUV matrix is also fixed after pre-training. This yields the Values matrix for the entire sequence.

8. Compute Context Vector: The attention weights (for the new token) are multiplied by the full Values matrix. This produces the context vector specifically for the new token. As previously established, only the context vector for the last token is needed to predict the next token.

9. Predict Next Token: The context vector for the new token is passed through the rest of the model's layers (feed-forward networks, etc., and eventually the output projection head) to generate the logits, from which the next token is predicted.

Benefits of Multi-Head Latent Attention

MHLA offers significant advantages due to this latent space projection and absorption trick:

• Dramatic Reduction in KV Cache Size: Only one matrix (CKV) needs to be cached, not separate Keys and Values matrices. The dimension of this single cached matrix is determined by a chosen latent dimension (DL), which is significantly smaller than the N x H dimension of traditional keys/values. For DeepSeek's model, replacing the 2 x N x H dimension with a single DL of 576 (compared to 2 x 128 x 128) resulted in a 57 times reduction in KV Cache size, bringing the required memory down from 400 GB to roughly 6 GB. This substantially lowers inference costs and improves efficiency.

• Maintained Performance: Crucially, MHLA does not share key or value content across different attention heads. While the CKV cache is single, the Keys are derived by multiplying CKV with WUK, and Values are derived by multiplying CKV with WUV. Since WUK and WUV have different trainable weights for each attention head, the resulting Keys and Values matrices are distinct for every head. This preserves the diversity of information capture across heads that is essential for strong performance and context understanding, unlike MQA or GQA where heads or groups share content.

In essence, DeepSeek's Multi-Head Latent Attention effectively decouples the memory requirement (driven by the low-dimensional latent cache) from the performance aspect (maintained by head-specific projection weights WUK/WUV), achieving both efficiency and strong performance. This innovation is described as a "beautiful thing" and a "magic bullet" for solving the KV cache problem without sacrificing performance.